Mixed numbers combine whole numbers and proper fractions, while improper fractions represent whole quantities as single fractions. Converting between them simplifies calculations and enhances fraction understanding. Printable PDF worksheets offer practice opportunities for mastering these essential math skills.
1.1 Definition of Mixed Numbers
A mixed number is a mathematical expression that combines a whole number and a proper fraction. It represents a value greater than one but less than the next whole number. For example, in the mixed number 3 1/2, 3 is the whole number, and 1/2 is the proper fraction. Mixed numbers are useful for showing quantities that are not whole but include a partial amount. They are widely used in real-world applications, such as cooking, construction, and everyday measurements, making them an essential concept in fraction operations.
1.2 Definition of Improper Fractions

An improper fraction is a type of fraction where the numerator is greater than or equal to the denominator. This means the fraction represents a value of one or more. For example, 5/4 is an improper fraction because the numerator 5 is larger than the denominator 4. Improper fractions are often used in mathematical operations because they simplify calculations. They can easily be converted to mixed numbers for real-world applications, making them a fundamental concept in understanding and working with fractions.
1.3 Importance of Converting Between Mixed Numbers and Improper Fractions
Converting between mixed numbers and improper fractions is crucial for simplifying mathematical operations. Mixed numbers are easier for real-world applications, while improper fractions are preferred in algebraic calculations. This conversion ensures accuracy in tasks like addition, subtraction, and multiplication of fractions. Worksheets provide structured practice, helping students master the process and build a strong foundation in fraction operations. Proficiency in these conversions enhances problem-solving skills and prepares students for advanced math concepts.
Step-by-Step Guide to Converting Mixed Numbers to Improper Fractions
Learn to convert mixed numbers to improper fractions with clear, structured steps. Understand the components, multiply, add, and place the result over the original denominator for accuracy.
2.1 Understanding the Components of a Mixed Number
A mixed number consists of a whole number and a proper fraction. For example, in the mixed number 3 1/2, 3 is the whole number, and 1/2 is the fractional part. Recognizing these components is crucial for conversion. The whole number represents complete units, while the fraction shows a part of another unit. Understanding this structure helps in applying the correct steps to convert mixed numbers into improper fractions. This foundational knowledge ensures accuracy in performing the conversion process effectively.
2.2 Multiplying the Whole Number by the Denominator
To convert a mixed number to an improper fraction, start by multiplying the whole number by the denominator. For example, in 3 1/2, multiply 3 (the whole number) by 2 (the denominator), resulting in 6. This step establishes the base for the new numerator in the improper fraction. Accurately performing this multiplication is essential for maintaining the value of the original mixed number. Ensure the calculation is precise to avoid errors in the subsequent steps of the conversion process.
2.3 Adding the Numerator to the Product
After multiplying the whole number by the denominator, the next step is to add the numerator of the fractional part to this product. For instance, in the mixed number 3 1/2, after multiplying 3 by 2 to get 6, you then add the numerator 1 to 6, resulting in 7. This sum becomes the new numerator of the improper fraction, while the denominator remains unchanged. Accurate addition here is crucial for maintaining the correct value of the original mixed number in its improper fraction form.
2.4 Placing the Result Over the Original Denominator
After obtaining the sum from adding the numerator to the product, the final step is to place this result over the original denominator. This creates the improper fraction. For example, if you have the mixed number 3 1/2, and after multiplying and adding you get 7, you place 7 over the original denominator 2, resulting in the improper fraction 7/2. This step ensures the fraction accurately represents the original mixed number’s value in a single, simplified form.
Benefits of Using Worksheets for Practice
Worksheets provide structured practice, helping users master mixed number to improper fraction conversions. They offer clear formats and organized learning experiences, enhancing understanding and retention of fraction concepts.
3.1 Reinforcing Mathematical Concepts
Worksheets dedicated to converting mixed numbers to improper fractions provide structured practice, ensuring a deep understanding of fraction relationships. By repeatedly applying conversion steps, users solidify their grasp of how whole numbers and fractions interact. Clear examples and step-by-step solutions guide learners, while varied problem sets prevent memorization and promote critical thinking. Visual aids, such as diagrams, further enhance comprehension, making abstract concepts tangible. Regular practice with these resources builds confidence and fluency in fraction operations, essential for advanced math topics. Printable PDF formats make these tools accessible for offline study, catering to different learning preferences and environments.
3.2 Developing Problem-Solving Skills
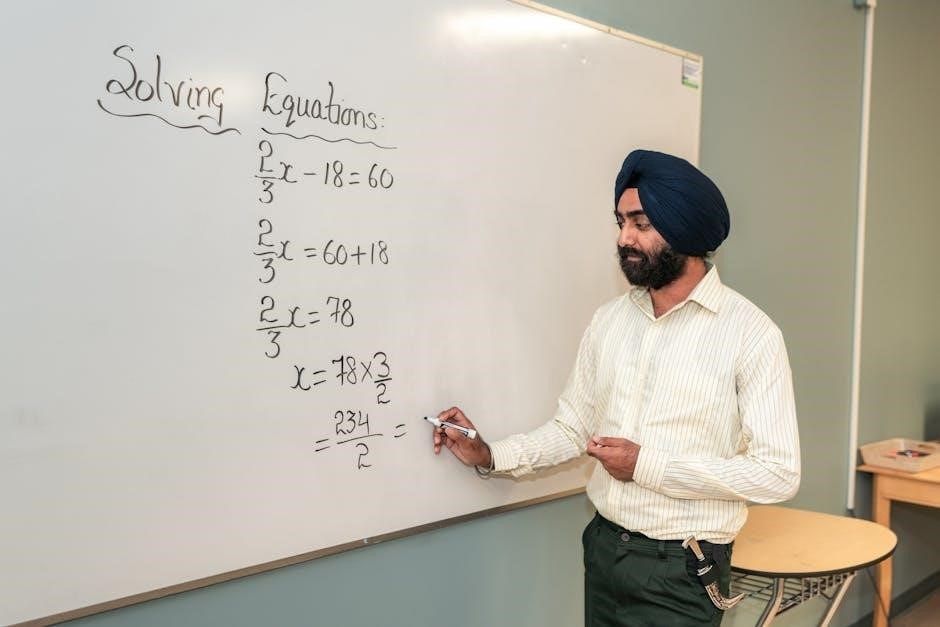
Engaging with mixed number to improper fraction worksheets enhances problem-solving abilities by presenting diverse numerical scenarios. These exercises encourage learners to apply conversion steps methodically, fostering analytical thinking. The structured format of worksheets helps users identify patterns and relationships between whole numbers and fractions. By tackling multiple problems, individuals refine their logical reasoning and mathematical accuracy. Step-by-step solutions provide guidance, while challenging problems promote independent thinking. This practice not only strengthens fraction conversion skills but also builds resilience and confidence in approaching complex math problems.
3.3 Building Confidence in Fraction Operations
Mastering mixed number to improper fraction conversions through worksheets boosts confidence in handling fractions. Regular practice helps learners grasp the underlying principles, reducing anxiety during math tasks. The clear structure of worksheets allows users to track their progress, celebrating small victories that enhance self-assurance. As skills improve, students become more comfortable applying these concepts to real-world problems, fostering a positive attitude toward mathematics. The availability of step-by-step solutions and varied difficulty levels ensures that learners can build their confidence gradually and effectively.
How to Create Effective Mixed Number to Improper Fraction Worksheets
Design clear, concise problems with visual aids to enhance understanding. Include step-by-step solutions for guidance and offer customizable options to cater to different skill levels and learning needs.
4.1 Designing Clear and Concise Problems
Creating effective worksheets begins with designing clear and concise problems. Use simple language and avoid clutter to ensure focus on the mathematical concept. Include examples that gradually increase in difficulty, starting with basic mixed numbers and progressing to more complex ones. Provide step-by-step solutions or hints to guide learners, especially for improper fraction conversions. Ensure problems are aligned with curriculum standards and cater to different skill levels. Incorporate visual aids like diagrams or number lines to enhance understanding. Clear instructions and organized layouts help students stay focused and engaged during practice.
4.2 Incorporating Visual Aids
Visual aids are essential for making worksheets engaging and effective. Use diagrams, number lines, or pie charts to illustrate the relationship between mixed numbers and improper fractions. Highlight key steps, such as multiplying the whole number by the denominator, to help students follow the process. Include examples with shaded areas or arrows to show how whole numbers and fractions combine. Visual representations make abstract concepts more concrete, especially for visual learners. Ensure images are clear, labeled, and directly tied to the problems to avoid confusion and enhance understanding.
4.3 Providing Step-by-Step Solutions
Step-by-step solutions are crucial for helping students master fraction conversions. Break down each problem into clear, manageable parts, showing how to multiply the whole number by the denominator, add the numerator, and place the result over the original denominator. Include visual cues like arrows or highlighting to guide students through the process. Offer explanations for common errors, such as forgetting to multiply or misplacing the numerator. Providing detailed solutions in PDF worksheets allows students to review and practice independently, reinforcing their understanding and building confidence in converting mixed numbers to improper fractions effectively.

Tips for Teaching Mixed Number to Improper Fraction Conversion
Use real-world examples to illustrate concepts, encourage peer-to-peer learning for collaborative problem-solving, and utilize digital tools for interactive practice to enhance understanding and engagement in fraction conversions.
5.1 Using Real-World Examples
Using real-world examples, such as cooking recipes or construction materials, helps students understand the practical relevance of converting mixed numbers to improper fractions. For instance, measuring ingredients like 1 1/2 cups of flour can be converted to 3/2 cups, simplifying calculations. Relatable scenarios make abstract concepts more tangible, fostering better comprehension. Encourage students to identify similar situations in their daily lives where fractions are used, reinforcing their ability to apply mathematical skills practically. This approach not only enhances understanding but also builds confidence in handling fraction operations effectively.
5.2 Encouraging Peer-to-Peer Learning
Encouraging peer-to-peer learning fosters a collaborative environment where students can teach and learn from one another. Pairing students to work on mixed number to improper fraction worksheets allows them to discuss concepts, share strategies, and clarify doubts. This method not only strengthens understanding but also builds communication and teamwork skills. Students can explain their problem-solving processes, reinforcing their own knowledge while helping others. Peer learning also promotes confidence, as students see their ability to teach and guide their peers effectively. Utilizing worksheets as a shared resource enhances this collaborative approach, making learning interactive and engaging for everyone involved.
5.3 Utilizing Digital Tools for Practice
Digital tools offer interactive and engaging ways to practice converting mixed numbers to improper fractions. Online worksheets, math apps, and educational websites provide step-by-step guides and real-time feedback, enhancing learning. Video tutorials and interactive simulations help visualize the conversion process, making it easier for students to grasp. Additionally, downloadable PDF resources and customizable worksheets allow for personalized practice. These tools cater to different learning styles and skill levels, ensuring a comprehensive understanding of fraction conversions. By leveraging technology, students can practice anytime, anywhere, reinforcing their skills in a dynamic and accessible manner.
Common Mistakes to Avoid
Common errors include forgetting to multiply the whole number by the denominator, incorrect addition or subtraction, and misplacing the resulting numerator. Double-checking work helps prevent these mistakes.

6.1 Forgetting to Multiply the Whole Number by the Denominator
One of the most frequent errors when converting mixed numbers to improper fractions is omitting the multiplication of the whole number by the denominator. This step is crucial because it determines the overall value of the fraction. For example, in the mixed number 3 1/2, the whole number (3) must be multiplied by the denominator (2) to get 6. Adding the numerator (1) gives 7, resulting in the improper fraction 7/2. Forgetting this step leads to incorrect results, so always double-check your calculations to ensure accuracy and proper conversion.
6.2 Incorrectly Adding or Subtracting Numbers

A common mistake when converting mixed numbers to improper fractions is incorrectly adding or subtracting numbers. For instance, in the mixed number 3 1/2, some students might add the whole number (3) and the denominator (2) instead of multiplying them. This leads to an incorrect numerator. Always remember to multiply the whole number by the denominator first, then add the numerator. For example, 3 * 2 = 6, plus 1 equals 7, resulting in the improper fraction 7/2. Double-checking your work can help prevent such errors and ensure accurate conversions.

6.3 Misplacing the Resulting Numerator
Another common error is misplacing the resulting numerator when converting mixed numbers to improper fractions. For example, when converting 3 1/2, some students might incorrectly place the numerator over the wrong denominator or forget the denominator entirely. Always ensure the numerator is placed over the original denominator. For instance, 3 1/2 becomes (3*2 + 1)/2 = 7/2. Misplacing the numerator leads to incorrect fractions, so double-checking your work is essential. Using worksheets or online resources can help reinforce proper placement and reduce errors in fraction conversions.

Printable Mixed Number to Improper Fraction Worksheets
Find free PDF resources online for mixed number to improper fraction practice. Customize worksheets for different skill levels and ensure clarity for easy understanding and readability.
7.1 Finding Free PDF Resources Online
Free PDF resources for mixed number to improper fraction worksheets are widely available online. Websites like MathSalamanders and others offer downloadable sheets tailored for various grade levels. These worksheets often include step-by-step solutions and examples, making them ideal for self-study or classroom use. Simply search for “mixed number to improper fraction worksheet PDF” to find numerous options. Many resources are designed to be printer-friendly, ensuring clarity and readability. Utilize these tools to practice and master fraction conversions with ease and convenience.
7.2 Customizing Worksheets for Different Skill Levels
Worksheets for mixed number to improper fraction conversions can be tailored to suit various skill levels. For beginners, problems with smaller numbers and simpler fractions are ideal. Advanced learners can tackle larger numbers and complex fractions. Many PDF resources allow customization, enabling teachers or parents to select difficulty levels and focus on specific concepts. Incorporating step-by-step solutions and visual aids enhances understanding. Customizable worksheets ensure that learners receive targeted practice, making the learning process more effective and engaging. This adaptability helps cater to diverse educational needs and promotes mastery of fraction conversions at every level.
7.3 Ensuring Clarity and Readability
Clarity and readability are crucial for effective learning. Mixed number to improper fraction worksheets should use clear fonts, proper spacing, and consistent formatting. High-quality PDFs ensure that fractions and numbers are easily distinguishable. Visual aids, such as diagrams or number lines, can enhance understanding. Proper alignment of whole numbers and fractions helps avoid confusion. Worksheets should also include clear instructions and examples. By prioritizing readability, learners can focus on the math without being distracted by poor formatting. This attention to detail makes practice more efficient and enjoyable for students of all ages and skill levels.

Conclusion
Mastering mixed numbers and improper fractions is essential for math proficiency. Regular practice with worksheets enhances understanding and confidence. Keep practicing to achieve mastery!
8.1 Summary of Key Concepts

Converting mixed numbers to improper fractions involves multiplying the whole number by the denominator, adding the numerator, and placing the result over the original denominator. This process simplifies calculations and enhances understanding of fraction relationships. Worksheets, both printable and online, provide structured practice to reinforce these skills. They often include step-by-step solutions, catering to different learning needs. Regular practice with these resources helps build confidence and fluency in fraction operations. By mastering this conversion, students gain a stronger foundation in mathematics, enabling them to tackle more complex problems with ease.
8.2 Encouragement for Continued Practice
Consistent practice is key to mastering mixed number and improper fraction conversions. Regular use of worksheets, especially in PDF format, helps reinforce these skills and builds confidence. Encourage students to explore free online resources, such as those from Math Salamanders, to access a variety of practice materials. Celebrate progress, no matter how small, to maintain motivation. Emphasize the importance of understanding these concepts, as they form the foundation for more complex math problems. With dedication and the right tools, students can achieve fluency in fraction conversions and excel in their mathematical journey.
8.3 Final Thoughts on Mastering Fraction Conversions
Mastery of converting mixed numbers to improper fractions is a fundamental math skill that enhances problem-solving abilities. Consistent practice using worksheets, especially in PDF format, ensures long-term retention. Utilize online resources like Math Salamanders for diverse practice materials. Understanding the “why” behind each step fosters a deeper grasp of fractions. Encourage learners to explore real-world applications, making the concept more relatable. With patience and dedication, students can confidently navigate fraction conversions, paving the way for success in advanced mathematical concepts. Celebrate small victories and remind learners that mastery is a rewarding journey.
